Our research target is to reveal the peculiar electronic, magnetic and transport properties in nano-carbon materials such as graphene, nano-graphene, graphene nanoribbons, nanotubes using theoretical and/or computation method.
 

Recently graphene, a single-layer of graphite, has attracted much attention both from the fundamental and applied sciences. In graphene, carbon atoms form a honeycomb lattice structure as shown in Fig.1. Due to this structure, the electronic states of graphene are described by the massless Dirac Fermion in sharp contrast with the conventional two-dimensional electron gas on the semiconductor devices. Such unconventional electronic states are the sources of the peculiar electronic properties of graphene, which are characterized as the half-integer quantum Hall effect, the absence of backward scattering, Klein tunneling and ultrahigh mobility of electrons.
 

Figure 1: Lattice structure of graphene

Figure 2 shows the energy dispersion of graphene to the momentum near the Fermi energy and corresponding density of states (DOS). In graphene, energy is linearly proportional to the momentum. The valence and conduction bands conically touch at E=0 (Fermi energy). Thus, DOS becomes zero at E=0 and linearly increases with increase of energy. However, in conventional two-dimensional gas, the energy is proportional to the squre of the momentum.
 

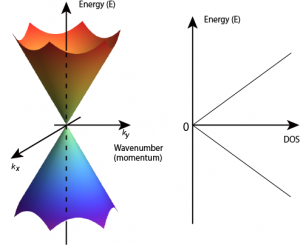
Figure 2: Energy dispersion of graphene near the Fermi energy and corresponding density of states (DOS)

The successive miniaturization of the graphene electronic devices inevitably demands the clarification of edge effects on the electronic structures, electronic transport and magnetic properties of nanometer-sized graphene. The presence of edges in graphene has strong implications for the low-energy spectrum of the p-electrons.
 

There are two basic shapes of edges, armchair and zigzag, as shown in Figs. 3 (a) and (b). For graphene with an armchair edge, linear energy dispersion appears same as in graphene sheet (Fig. 3(c)). However, if graphene has a zigzag edge, an additional flat energy dispersion appears at E=0. Since this flat energy dispersion produces a sharp peak in DOS at the Fermi energy, the presence of zigzag edges strongly modifies the electronic states of graphene.
 

In 1996, Fujita, Wakabayashi, Nakada and Kusakabe have shown that the origin of the flat energy dispersion is due to the localized edge states of electrons. These edge states correspond to the non-bonding configurations. In contrast, edge states are completely absent for ribbons with armchair edges. Recent experiments support the evidence of edge localized states. Also, it has been recently reported by several overseas groups that graphene nanoribbons can experimentally be produced by using lithography techniques and chemical techniques.
 

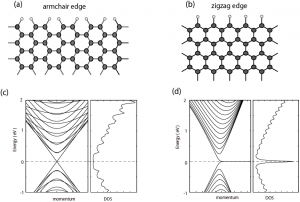
Figure 3: Lattice structure of graphene with (a) an armchair edge and (b) a zigzag edge. Here carbon atoms (black circles) at edges are terminated by hydrogen atom (white circle). Energy dispersion for graphene with (c) an armchair edge and (d) a zigzag edge, together with the corresponding DOSs.

On the background mentioned above, the main purpose of our research is to clarify the peculiar features in electronic, magnetic and transport properties of nano- and meso-scopic systems based on carbon materials. Also, we aim to design and explore theoretically the new functionalities as the next-generation devices based on the peculiar electronic properties.