Topological photonic crystals with zero Berry curvature
Feng Liu, Hai-Yao Deng, and Katsunori Wakabayashi
Phys. Rev. B 97, 035442 – Published 31 January 2018
https://doi.org/10.1103/PhysRevB.97.035442
ABSTRACT
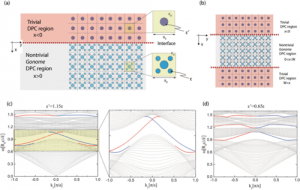
Topological photonic crystals are designed based on the concept of Zak’s phase rather than the topological invariants such as the Chern number and spin Chern number, which rely on the existence of a nonvanishing Berry curvature. Our photonic crystals (PCs) are made of pure dielectrics and sit on a square lattice obeying the C4v point-group symmetry. Two varieties of PCs are considered: one closely resembles the electronic two-dimensional Su-Schrieffer-Heeger model, and the other continues as an extension of this analogy. In both cases, the topological transitions are induced by adjusting the lattice constants. Topological edge modes (TEMs) are shown to exist within the nontrivial photonic band gaps on the termination of those PCs. The high efficiency of these TEMs transferring electromagnetic energy against several types of disorders has been demonstrated using the finite-element method.